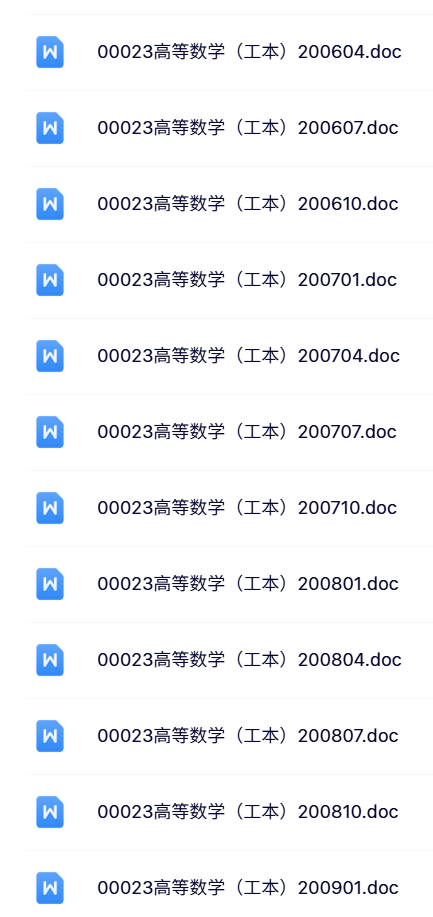
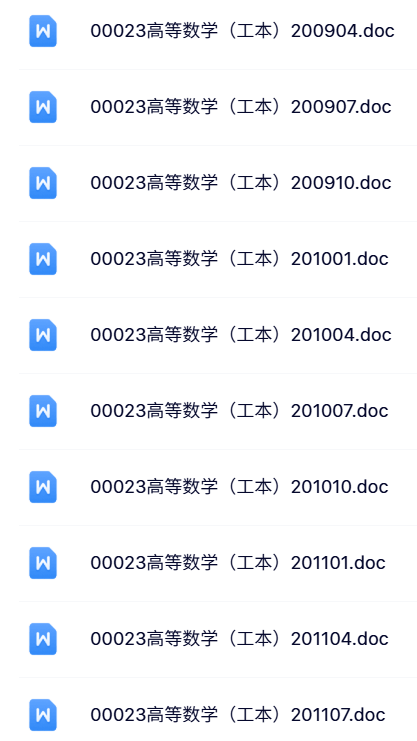
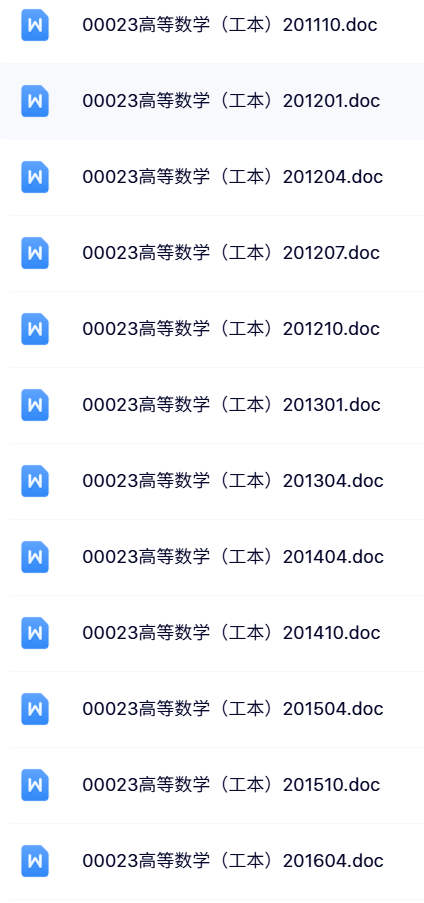
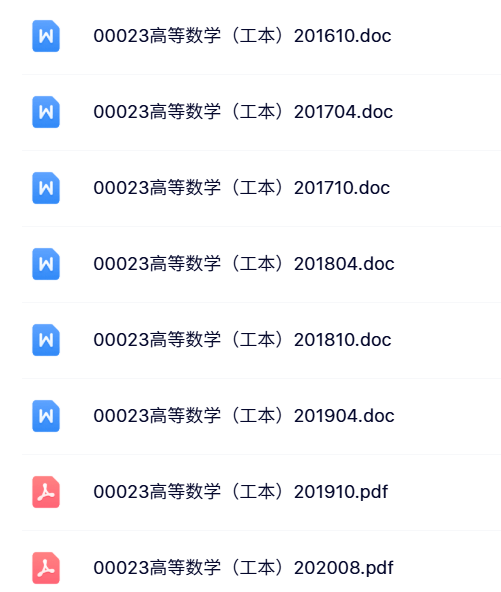
资料目录(截图原因可能偏模糊,实际都是高清版)


备考高等教育自学考试《高等数学(工本)》是一项系统工程,需要清晰的规划、扎实的努力与恰当的方法。这门课程不仅内容深、覆盖面广,而且对逻辑思维与计算能力要求较高,但只要方法得当,完全可以通过系统备考顺利通过。
一、 精研大纲,明确核心 备考第一步,必须是深入研读最新的官方考试大纲。大纲是考试的“宪法”,它会清晰列出各章节的考核要求(识记、领会、简单应用、综合应用)、分数占比以及考试题型。将大纲与教材目录对照,标出重点章节(如多元函数微积分、常微分方程、空间解析几何与向量代数、无穷级数等通常是重中之重),做到心中有地图,复习不盲目。
二、 教材为本,构建体系 切勿脱离教材。自考有其指定的官方教材,必须从头至尾精读至少两遍。第一遍通读,理解基本概念、定理和公式的来源与含义,在笔记本上梳理出每一章的知识框架图。第二遍结合课后习题精读,力求吃透例题的解题思路和步骤。工科数学重在应用,对关键公式(如格林公式、高斯公式、傅里叶级数展开等)的适用条件和推导过程要有清晰理解,而非死记硬背。
三、 勤练真题,把握规律 历年真题是最宝贵的备考资源。建议在完成章节复习后,按章节练习近5-10年的真题,检测学习效果,了解常见考点。考前1-2个月,进行整套试卷的模拟考试,严格计时。通过分析真题,可以直观感受命题风格、难度分布和重复考点,许多计算题题型和证明思路都有很高的重现率。对错题务必建立专属集,反复钻研,直至彻底掌握。
四、 归纳总结,克服难点 高等数学(工本)的难点往往集中在曲线曲面积分、幂级数求解、微分方程应用等方面。对于这些“硬骨头”,需要单独进行专题总结,对比不同方法的异同(例如对坐标的曲线积分与对面积的曲面积分计算方法有何区别),归纳解题的固定步骤和易错点。可以借助一些高质量的辅导资料或网络课程,帮助理解抽象概念。
五、 持之以恒,保持状态 数学学习具有连续性,切忌三天打鱼两天晒网。制定一个切实可行的周计划,每天保持2-3小时的高效学习。公式需要反复记忆,解题手感需要持续保持。考前调整好心态,相信通过系统扎实的复习,你已经构建起了完整的知识体系,足以从容应对挑战。
总之,备考之路没有捷径,成功=理解大纲+吃透教材+苦练真题+善做总结。坚持下去,你不仅能通过考试,更能切实提升自己的数学思维与工程应用能力。祝你备考顺利,一举成功!
